On latent dynamics learning in nonlinear reduced order modeling

Abstract

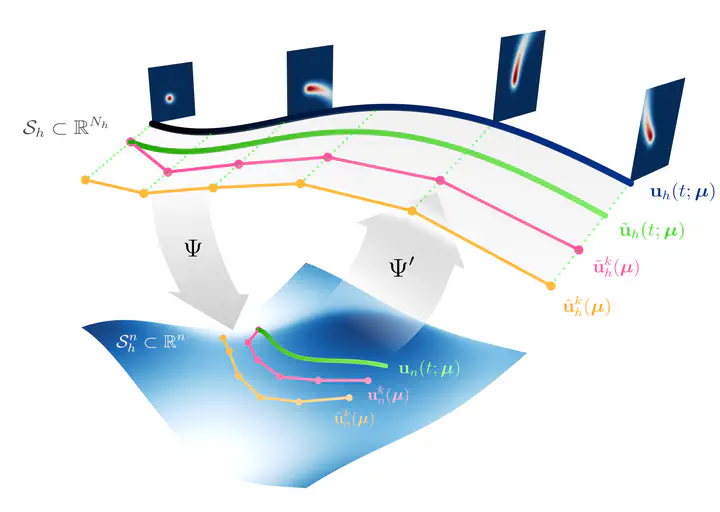
In this work, we present the novel mathematical framework of latent dynamics models (LDMs) for reduced order modeling of parameterized nonlinear time-dependent PDEs. Our framework casts this latter task as a nonlinear dimensionality reduction problem, while constraining the latent state to evolve accordingly to an unknown dynamical system. A time-continuous setting is employed to derive error and stability estimates for the LDM approximation of the full order model (FOM) solution. We analyze the impact of using an explicit Runge-Kutta scheme in the time-discrete setting, resulting in the $\delta$LDM formulation, and further explore the learnable setting, $\delta$LDM$_\theta$, where deep neural networks approximate the discrete LDM components, while providing a bounded approximation error with respect to the FOM.

Stefania Fresca

Assistant Professor

My research interests are scientific machine learning, reduced order modeling and AI.