Error estimates for POD-DL-ROMs: a deep learning framework for reduced order modeling of nonlinear parametrized PDEs enhanced by proper orthogonal decomposition

Abstract

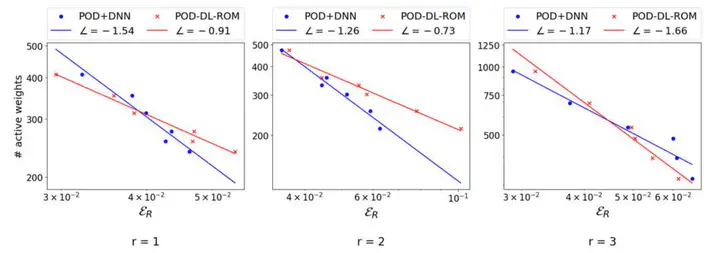
POD-DL-ROMs have been recently proposed as an extremely versatile strategy to build accurate and reliable reduced order models (ROMs) for nonlinear parametrized partial differential equations, combining (i) a preliminary dimensionality reduction obtained through proper orthogonal decomposition (POD) for the sake of efficiency, (ii) an autoencoder architecture that further reduces the dimensionality of the POD space to a handful of latent coordinates, and (iii) a dense neural network to learn the map that describes the dynamics of the latent coordinates as a function of the input parameters and the time variable. Within this work, we aim at justifying the outstanding approximation capabilities of POD-DL-ROMs by means of a thorough error analysis, showing how the sampling required to generate training data, the dimension of the POD space, and the complexity of the underlying neural networks, impact on the solution accuracy. This decomposition, combined with the constructive nature of the proofs, allows us to formulate practical criteria to control the relative error in the approximation of the solution field of interest, and derive general error estimates. Furthermore, we show that, from a theoretical point of view, POD-DL-ROMs outperform several deep learning-based techniques in terms of model complexity. Finally, we validate our findings by means of suitable numerical experiments, ranging from parameter-dependent operators analytically defined to several parametrized PDEs.

Stefania Fresca

Assistant Professor

My research interests are scientific machine learning, reduced order modeling and AI.