Deep-HyROMnet: A deep learning-based operator approximation for hyper-reduction of nonlinear parametrized PDEs

Abstract

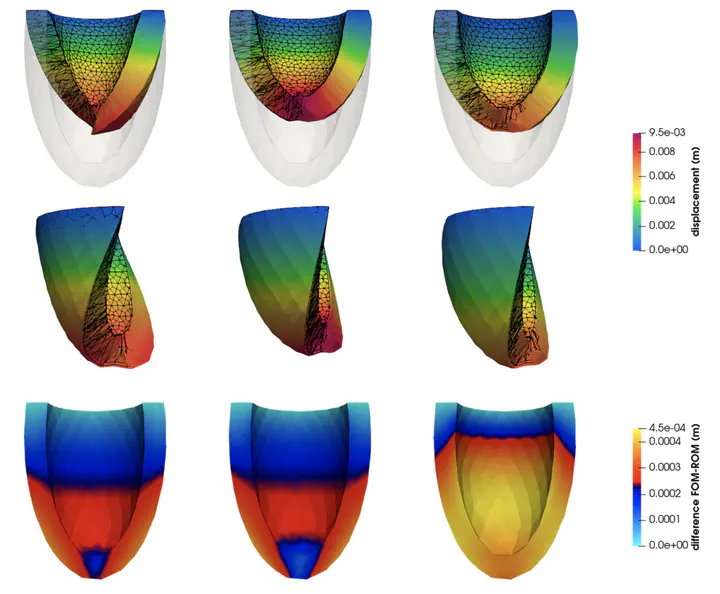
To speed-up the solution of parametrized differential problems, reduced order models (ROMs) have been developed over the years, including projection-based ROMs such as the reduced- basis (RB) method, deep learning-based ROMs, as well as surrogate models obtained through machine learning techniques. Thanks to its physics-based structure, ensured by the use of a Galerkin projection of the full order model (FOM) onto a linear low-dimensional subspace, the Galerkin-RB method yields approximations that fulfill the differential problem at hand. However, to make the assembling of the ROM independent of the FOM dimension, intru- sive and expensive hyper-reduction techniques, such as the discrete empirical interpolation method (DEIM), are usually required, thus making this strategy less feasible for problems characterized by (high-order polynomial or nonpolynomial) nonlinearities. To overcome this bottleneck, we propose a novel strategy for learning nonlinear ROM operators using deep neu- ral networks (DNNs). The resulting hyper-reduced order model enhanced by DNNs, to which we refer to as Deep-HyROMnet, is then a physics-based model, still relying on the RB method approach, however employing a DNN architecture to approximate reduced residual vectors and Jacobian matrices once a Galerkin projection has been performed. Numerical results dealing with fast simulations in nonlinear structural mechanics show that Deep-HyROMnets are orders of magnitude faster than POD-Galerkin-DEIM ROMs, still ensuring the same level of accuracy.

Stefania Fresca

Assistant Professor

My research interests are scientific machine learning, reduced order modeling and AI.