Projection-based reduced order models for parameterized nonlinear time-dependent problems arising in cardiac mechanics

Abstract

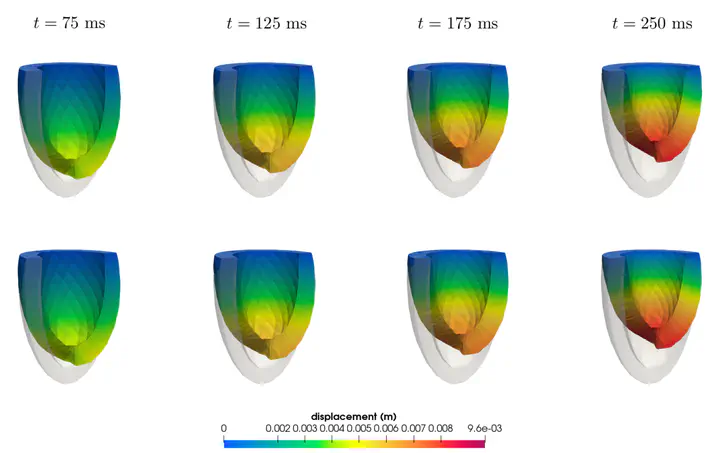
The numerical simulation of several virtual scenarios arising in cardiac mechanics poses a computational challenge that can be alleviated if traditional full-order models (FOMs) are replaced by reduced order models (ROMs). For example, in the case of problems involving a vector of input parameters related, e.g., to material coefficients, projection-based ROMs provide mathematically rigorous physics-driven surrogate ROMs. In this work we demonstrate how, once trained, ROMs yield extremely accurate predictions (according to a prescribed tolerance) – yet cheaper than the ones provided by FOMs – of the structural deformation of the left ventricular tissue over an entire heartbeat, and of related output quantities of interest, such as the pressure-volume loop, for any desired input parameter values within a prescribed parameter range. However, the construction of ROM approximations for time-dependent cardiac mechanics is not straightforward, because of the highly nonlinear and multiscale nature of the problem, and almost never addressed. Our approach relies on the reduced basis method for parameterized partial differential equations. This technique performs a Galerkin projection onto a low-dimensional space for the displacement variable; the reduced space is built from a set of solution snapshots – obtained for different input parameter values and time instances – of the high-fidelity FOM, through the proper orthogonal decomposition technique. Then, suitable hyper-reduction techniques, such as the Discrete Empirical Interpolation Method, are exploited to efficiently handle nonlinear and parameter-dependent terms. In this work we show how a fast and reliable approximation of the time-dependent cardiac mechanical model can be achieved by a projection-based ROM, taking into account both passive and active mechanics for the left ventricle providing all the building blocks of the methodology, and highlighting those challenging aspects that are still open.

Stefania Fresca

Assistant Professor

My research interests are scientific machine learning, reduced order modeling and AI.