Long-time prediction of nonlinear parametrized dynamical systems by deep learning-based reduced order models

Abstract

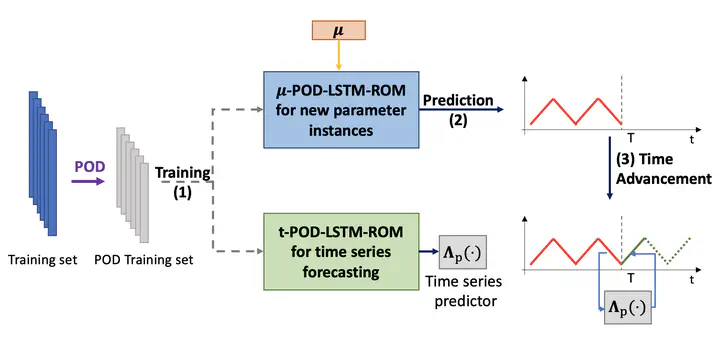
Deep learning-based reduced order models (DL-ROMs) have been recently proposed to overcome common limitations shared by conventional ROMs–built, e.g., through proper orthogonal decomposition (POD) – when applied to nonlinear time-dependent parametrized PDEs. In particular, POD-DL-ROMs can achieve an extremely good efficiency in the training stage and faster than real-time performances at testing, thanks to a prior dimensionality reduction through POD and a DL-based prediction framework. Nonetheless, they share with conventional ROMs unsatisfactory performances regarding time extrapolation tasks. This work aims at taking a further step towards the use of DL algorithms for the efficient approximation of parametrized PDEs by introducing the mut-POD-LSTM-ROM framework. This latter extends the POD-DL-ROMs by adding a two-fold architecture taking advantage of long short-term memory (LSTM) cells, ultimately allowing long-term prediction of complex systems’ evolution, with respect to the training window, for unseen input parameter values. Numerical results show that mut-POD-LSTM-ROMs enable the extrapolation for time windows up to 15 times larger than the training time interval, also achieving better performances at testing than POD-DL-ROMs.

Stefania Fresca

Assistant Professor

My research interests are scientific machine learning, reduced order modeling and AI.