Reduced order modeling of parametrized systems through autoencoders and SINDy approach: continuation of periodic solutions

Abstract

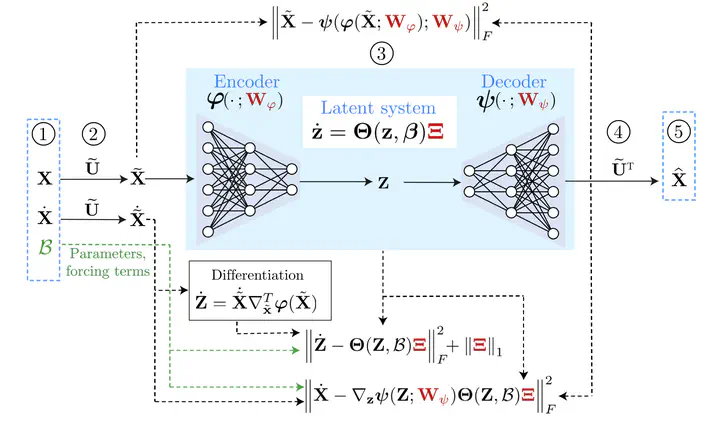
Highly accurate simulations of complex phenomena governed by partial differential equations (PDEs) typically require intrusive methods and entail expensive computational costs, which might become prohibitive when approximating steady-state solutions of PDEs for multiple combinations of control parameters and initial conditions. Therefore, constructing efficient reduced order models (ROMs) that enable accurate but fast predictions, while retaining the dynamical characteristics of the physical phenomenon as parameters vary, is of paramount importance. In this work, a data-driven, non-intrusive framework which combines ROM construction with reduced dynamics identification, is presented. Starting from a limited amount of full order solutions, the proposed approach leverages autoencoder neural networks with parametric sparse identification of nonlinear dynamics (SINDy) to construct a low-dimensional dynamical model. This model can be queried to efficiently compute full-time solutions at new parameter instances, as well as directly fed to continuation algorithms. These aim at tracking the evolution of periodic steady-state responses as functions of system parameters, avoiding the computation of the transient phase, and allowing to detect instabilities and bifurcations. Featuring an explicit and parametrized modeling of the reduced dynamics, the proposed data-driven framework presents remarkable capabilities to generalize with respect to both time and parameters. Applications to structural mechanics and fluid dynamics problems illustrate the effectiveness and accuracy of the proposed method.

Stefania Fresca

Assistant Professor

My research interests are scientific machine learning, reduced order modeling and AI.