Abstract
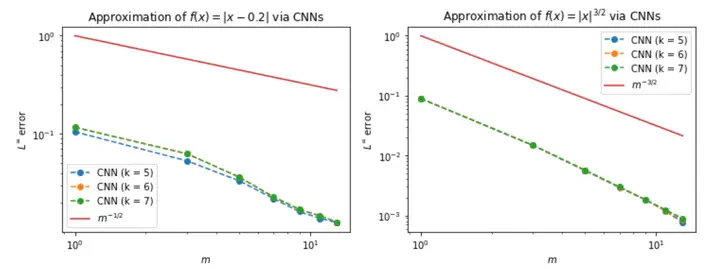
Recently, deep Convolutional Neural Networks (CNNs) have proven to be successful when employed in areas such as reduced order modeling of parametrized PDEs. Despite their accuracy and efficiency, the approaches available in the literature still lack a rigorous justification on their mathematical foundations. Motivated by this fact, in this paper we derive rigorous error bounds for the approximation of nonlinear operators by means of CNN models. More precisely, we address the case in which an operator maps a finite dimensional input onto a functional output, and a neural network model is used to approximate a discretized version of the input-to-output map. The resulting error estimates provide a clear interpretation of the hyperparameters defining the neural network architecture. All the proofs are constructive, and they ultimately reveal a deep connection between CNNs and the Fourier transform. Finally, we complement the derived error bounds by numerical experiments that illustrate their application.
Stefania Fresca
Assistant Professor
My research interests are scientific machine learning, reduced order modeling and AI.